Fisica II: tarea 2 1/2

Operaciones con vectores

Las operaciones que se pueden realizar con los vectores en el plano.

SUMA Y RESTA DE VECTORES

Dados dos vectores libres del plano, definiremos suma de estos vectores al vector resultante de unir el origen del primer vector con el extremo del segundo vector, haciendo coincidir previamente el extremo del primer vector con el origen del segundo vector. Gráficamente se puede ver el desarrollo de esta operación: escogeremos un representante del segundo vector libre cuyo origen sea el extremo del representante del primer vector libre. Justo después, se unirá el origen del primer vector con el extremo del segundo vector.

Geométricamente, podemos dibujar un paralelogramo con estos dos vectores, y la suma nos dará la diagonal de dicho paralelogramo.

Para hallar el producto de un vector por un escalar (control a para u; control b para v), bastará con multiplicar el punto extremo del vector, y después sumar las coordenadas de los puntos origen y extremo.

Gráficamente, consiste en prolongar el vector u a-veces sobre la misma recta sobre la que está el vector v.

COMBINACIÓN LINEAL DE VECTORES.

Si combinamos las dos operaciones anteriores, obtenemos combinaciones lineales de un conjunto de vectores. Dado un conjunto de vectores V ={u,v,w,s,t,…}, y un conjunto de escalares U = {a,b,c,d,e,…}decimos que una combinación lineal de vectores es toda expresión de la forma: a•u+b•v+c•w+d•s+e•t+…

Al hacer operaciones, el resultado final, es otro vector del plano. Se puede ver gráficamente en la escena cómo lo que hacemos es sumar dos nuevos vectores, obtenidos al multiplicarlos previamente por escalares.

PRODUCTO ESCALAR DE VECTORES

Para ello debemos definir un nuevo concepto: ÁNGULO QUE FORMAN DOS VECTORES.

El ángulo que forman dos vectores es el menor de los ángulos que definen las dos rectas sobre las que se encuentran dichos vectores.

Se define Producto escalar de los vectores u y v como el resultado de realizar las operaciones:

 u•v= |u|•|v|•cos(u,v)  donde |u| y |v| indican los

módulos de los vectores, y cos(u,v) es el coseno del ángulo que forman los dos vectores.

Gradiente

El gradiente de un campo escalar en un punto es un vector, definido como el único que permite hallar la derivada direccional en cualquier dirección como siendo un vector unitario y la derivada direccional de en la dirección , que informa de la tasa de variación del campo escalar al desplazarnos según esta dirección:

Una forma equivalente de definir el gradiente es como el único vector que, multiplicado por cualquier desplazamiento infinitesimal, da el diferencial del campo escalar:

Con la definición anterior, el gradiente está caracterizado de forma unívoca.

El gradiente se expresa alternativamente mediante el uso del operador nabla:

En esta imagen, el campo escalar se aprecia en blanco y negro, los cuales representan valores bajos o altos respectivamente, y el gradiente correspondiente se aprecia por flechas azules.

Divergencia

Divergencia de un campo mide la tendencia de dicho campo vectorial a originarse en o a converger hacia ciertos puntos. La divergencia de un campo vectorial es un campo escalar, y se define como el flujo del campo vectorial por unidad de volumen:

donde S es una superficie cerrada que se reduce a un punto en el límite. El símbolo representa el operador nabla.

Esta definición está directamente relacionada con el concepto de flujo del campo. Como en el caso del flujo, si la divergencia en un punto es positiva, se dice que el campo posee manantiales. Si la divergencia es negativa, se dice que tiene sumideros. El ejemplo más característico lo dan las cargas eléctricas, que dan la divergencia del campo eléctrico, siendo las cargas positivas manantiales y las negativas sumideros del campo eléctrico.

Magnitudes Escalares:

Son aquellas que quedan perfectamente definidas mediante un valor numérico, acompañado de la unidad de medida correspondiente.(Ver ejemplo 4.4.1).

Magnitudes Vectoriales:

Son aquellas en las que, además de un valor numérico, se necesitan otros detalles. Dirección, sentido y módulo son los requisitos necesarios para definirlas.

Ej.- Masa, tiempo, temperatura.

Ej.- Velocidad, aceleración, fuerza.

Se llaman fuentes escalares del campo 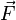al campo escalar que se obtiene a partir de la divergencia de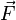

La divergencia de un campo vectorial se relaciona con el flujo a través del teorema de Gauss o teorema de la divergencia. Cuando la definición de divergencia se aplica al caso de un campo expresado en coordenadas cartesianas,

el resultado es sencillo

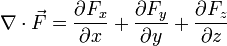
Sin embargo, para un caso más general de coordenadas curvilíneas, como las cilíndricas o las esféricas, la expresión se complica debido a la dependencia de los vectores de la base con la posición. La expresión para un sistema de coordenadas ortogonales es

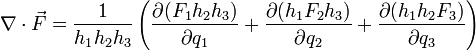
donde los hi son los factores de escala del sistema. Esta fórmula general, para el caso de coordenadas cartesianas (hx = hy = hz = 1) se reduce a la expresión anterior. Para coordenadas cilíndricas ( 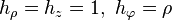) resulta